Multiwfn forum
Multiwfn official website: //www.umsyar.com/multiwfn. Multiwfn forum in Chinese: http://bbs.keinsci.com/wfn
You are not logged in.
- Topics:Active|Unanswered
Pages:1
#2Re:Multiwfn and wavefunction analysis»Transition Density Matrix Elements analysis of Multiwfn»2021-12-21 03:43:34
Thank you very much.
#3Re:Multiwfn and wavefunction analysis»Transition Density Matrix Elements analysis of Multiwfn»2021-12-20 08:01:28
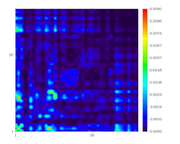
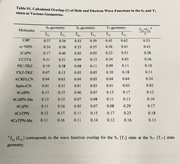
There is no issue with this heatmap in sense of presentation. I have also published many articles including this heatmaps and the above mentioned reference list also has my publications references. The only issue which often I met is the font size and style at the axis ends. Although, I have solved this issue many times to increase the sharpness of this heatmap in image form but as we edit the picture with different editing tools, the actuall resolution of the image has been decreased. You have mentioned the replot this heatmap in origin again, do you have any guiding article about this or any guidelines which deals how to replot this heatmap again in Origin with more resolution?
Please if you have guidelines about replot this heatmap in origin then share with us.
Thanks in Advance for your response
#4Multiwfn and wavefunction analysis»Transition Density Matrix Elements analysis of Multiwfn»2021-12-20 03:09:45
- Usman Ali
- Replies: 4
-
Hi Dr. Tian Lu!
Although the Multiwfn package is extremely of great importance in inter fragment charge transfer analysis (IFCT) but there is always a big reviewer's comments about the graphics provided by the Multiwfn mostly about the TDM heatmaps. I have tried alot to check that how we can edit the X, Y and Z-axis reading (to increase the font size, to change the font style and to increase the axis thickness).
Kindly tell me is there any source to do this like we can do in the case of UV-Visibile absorption spectra and also to save the text file to draw the spectrum in the origin with better styles.
Is there any way to solve the reviewer's comments on graphics provided by the Multiwfn?
Also guide us what information this text file provide us and how we can cite your article if we follow your guidelines by using any sobereva article rather than using software.
Can we cite your sobereva article?
I have also attached the Text file of this querry here.
1 1 0.016122
1 2 0.001315
1 3 0.014512
1 4 0.001165
1 5 0.000838
1 6 0.003480
1 7 0.000488
1 8 0.005869
1 9 0.001733
1 10 0.000564
1 11 0.004152
1 12 0.002013
1 13 0.007807
1 14 0.004710
1 15 0.000738
1 16 0.001086
1 17 0.002309
1 18 0.000526
1 19 0.000717
1 20 0.000225
1 21 0.000402
1 22 0.002900
1 23 0.001914
1 24 0.001965
1 25 0.005086
1 26 0.003628
1 27 0.003113
1 28 0.004637
1 29 0.001013
1 30 0.001535
1 31 0.002308
1 32 0.000461
1 33 0.001084
1 34 0.012962
1 35 0.006265
1 36 0.004986
1 37 0.000967
1 38 0.008079
1 39 0.001031
1 40 0.004152
1 41 0.001417
2 1 0.001315
2 2 0.016469
2 3 0.001179
2 4 0.000414
2 5 0.001402
2 6 0.008704
2 7 0.001401
2 8 0.002407
2 9 0.008216
2 10 0.000603
2 11 0.005815
2 12 0.018266
2 13 0.005102
2 14 0.004587
2 15 0.001566
2 16 0.006999
2 17 0.003142
2 18 0.003955
2 19 0.003467
2 20 0.006782
2 21 0.003863
2 22 0.000339
2 23 0.001500
2 24 0.001791
2 25 0.000252
2 26 0.000400
2 27 0.000605
2 28 0.000456
2 29 0.002923
2 30 0.001930
2 31 0.000230
2 32 0.002313
2 33 0.001273
2 34 0.006755
2 35 0.005267
2 36 0.002998
2 37 0.000906
2 38 0.005563
2 39 0.000758
2 40 0.002707
2 41 0.000603
3 1 0.014512
3 2 0.001179
3 3 0.013341
3 4 0.001117
3 5 0.001302
3 6 0.002906
3 7 0.000307
3 8 0.002559
3 9 0.004302
3 10 0.000971
3 11 0.007568
3 12 0.000961
3 13 0.004810
3 14 0.002360
3 15 0.000482
3 16 0.001844
3 17 0.001643
3 18 0.000353
3 19 0.000337
3 20 0.000266
3 21 0.000340
3 22 0.002268
3 23 0.001444
3 24 0.001087
3 25 0.003963
3 26 0.002551
3 27 0.002380
3 28 0.004403
3 29 0.000950
3 30 0.001103
3 31 0.002892
3 32 0.000116
3 33 0.000621
3 34 0.008839
3 35 0.004043
3 36 0.003364
3 37 0.000612
3 38 0.005295
3 39 0.000677
3 40 0.002746
3 41 0.001203
4 1 0.001165
4 2 0.000414
4 3 0.001117
4 4 0.001519
4 5 0.000735
4 6 0.000453
4 7 0.000090
4 8 0.000100
4 9 0.000525
4 10 0.000794
4 11 0.000523
4 12 0.000245
4 13 0.000464
4 14 0.000143
4 15 0.000146
4 16 0.000259
4 17 0.000153
4 18 0.000047
4 19 0.000030
4 20 0.000132
4 21 0.000059
4 22 0.000509
4 23 0.000192
4 24 0.000068
4 25 0.000219
4 26 0.000148
4 27 0.000228
4 28 0.000371
4 29 0.000373
4 30 0.000470
4 31 0.000256
4 32 0.000045
4 33 0.000143
4 34 0.000298
4 35 0.000200
4 36 0.000197
4 37 0.000017
4 38 0.000193
4 39 0.000046
4 40 0.000074
4 41 0.000093
5 1 0.000838
5 2 0.001402
5 3 0.001302
5 4 0.000735
5 5 0.001353
5 6 0.002399
5 7 0.000373
5 8 0.000122
5 9 0.000527
5 10 0.000062
5 11 0.000512
5 12 0.000471
5 13 0.000661
5 14 0.000171
5 15 0.000136
5 16 0.000193
5 17 0.000077
5 18 0.000319
5 19 0.000205
5 20 0.000093
5 21 0.000125
5 22 0.000140
5 23 0.000068
5 24 0.000207
5 25 0.000337
5 26 0.000066
5 27 0.000279
5 28 0.001337
5 29 0.000827
5 30 0.000396
5 31 0.000872
5 32 0.000080
5 33 0.000189
5 34 0.001395
5 35 0.000837
5 36 0.000594
5 37 0.000127
5 38 0.000980
5 39 0.000136
5 40 0.000495
5 41 0.000228
6 1 0.003480
6 2 0.008704
6 3 0.002906
6 4 0.000453
6 5 0.002399
6 6 0.004944
6 7 0.000385
6 8 0.001439
6 9 0.009576
6 10 0.001976
6 11 0.009293
6 12 0.006568
6 13 0.000373
6 14 0.002868
6 15 0.000706
6 16 0.004563
6 17 0.002418
6 18 0.001436
6 19 0.000943
6 20 0.003271
6 21 0.001964
6 22 0.000990
6 23 0.001485
6 24 0.000222
6 25 0.000473
6 26 0.000848
6 27 0.000143
6 28 0.000346
6 29 0.001395
6 30 0.000931
6 31 0.000913
6 32 0.000871
6 33 0.000526
6 34 0.001106
6 35 0.001049
6 36 0.000515
6 37 0.000183
6 38 0.000922
6 39 0.000145
6 40 0.000455
6 41 0.000027
7 1 0.000488
7 2 0.001401
7 3 0.000307
7 4 0.000090
7 5 0.000373
7 6 0.000385
7 7 0.002131
7 8 0.000643
7 9 0.002619
7 10 0.000298
7 11 0.000819
7 12 0.001558
7 13 0.001032
7 14 0.001463
7 15 0.001487
7 16 0.000725
7 17 0.000548
7 18 0.000181
7 19 0.000204
7 20 0.000436
7 21 0.000089
7 22 0.000126
7 23 0.000234
7 24 0.000118
7 25 0.000049
7 26 0.000069
7 27 0.000045
7 28 0.000075
7 29 0.000051
7 30 0.000077
7 31 0.000060
7 32 0.000184
7 33 0.000100
7 34 0.000632
7 35 0.000599
7 36 0.000353
7 37 0.000077
7 38 0.000366
7 39 0.000061
7 40 0.000216
7 41 0.000008
8 1 0.005869
8 2 0.002407
8 3 0.002559
8 4 0.000100
8 5 0.000122
8 6 0.001439
8 7 0.000643
8 8 0.002166
8 9 0.000295
8 10 0.001807
8 11 0.001680
8 12 0.004177
8 13 0.006997
8 14 0.001531
8 15 0.000965
8 16 0.000287
8 17 0.000556
8 18 0.000648
8 19 0.000809
8 20 0.000467
8 21 0.000422
8 22 0.000738
8 23 0.000700
8 24 0.001337
8 25 0.001438
8 26 0.000431
8 27 0.001434
8 28 0.000838
8 29 0.000587
8 30 0.000284
8 31 0.000341
8 32 0.000296
8 33 0.000247
8 34 0.004533
8 35 0.002684
8 36 0.001953
8 37 0.000423
8 38 0.003066
8 39 0.000416
8 40 0.001524
8 41 0.000850
9 1 0.001733
9 2 0.008216
9 3 0.004302
9 4 0.000525
9 5 0.000527
9 6 0.009576
9 7 0.002619
9 8 0.000295
9 9 0.001681
9 10 0.000213
9 11 0.001202
9 12 0.002128
9 13 0.001445
9 14 0.001135
9 15 0.000644
9 16 0.000349
9 17 0.000338
9 18 0.001760
9 19 0.000886
9 20 0.000424
9 21 0.000831
9 22 0.000141
9 23 0.000207
9 24 0.000647
9 25 0.000847
9 26 0.000069
9 27 0.000611
9 28 0.001476
9 29 0.001795
9 30 0.001184
9 31 0.000762
9 32 0.000380
9 33 0.000606
9 34 0.004843
9 35 0.002952
9 36 0.001986
9 37 0.000501
9 38 0.003506
9 39 0.000456
9 40 0.001763
9 41 0.000634
10 1 0.000564
10 2 0.000603
10 3 0.000971
10 4 0.000794
10 5 0.000062
10 6 0.001976
10 7 0.000298
10 8 0.001807
10 9 0.000213
10 10 0.002085
10 11 0.001071
10 12 0.000156
10 13 0.000518
10 14 0.000300
10 15 0.000487
10 16 0.000090
10 17 0.000095
10 18 0.000143
10 19 0.000045
10 20 0.000109
10 21 0.000008
10 22 0.000470
10 23 0.000058
10 24 0.000049
10 25 0.000095
10 26 0.000072
10 27 0.000138
10 28 0.000234
10 29 0.000288
10 30 0.000628
10 31 0.000053
10 32 0.000125
10 33 0.000302
10 34 0.000958
10 35 0.000509
10 36 0.000398
10 37 0.000099
10 38 0.000560
10 39 0.000079
10 40 0.000294
10 41 0.000027
11 1 0.004152
11 2 0.005815
11 3 0.007568
11 4 0.000523
11 5 0.000512
11 6 0.009293
11 7 0.000819
11 8 0.001680
11 9 0.001202
11 10 0.001071
11 11 0.002889
11 12 0.002857
11 13 0.002101
11 14 0.000525
11 15 0.000788
11 16 0.000519
11 17 0.000324
11 18 0.001429
11 19 0.000813
11 20 0.000771
11 21 0.000469
11 22 0.000196
11 23 0.000330
11 24 0.000848
11 25 0.001295
11 26 0.000477
11 27 0.000567
11 28 0.001974
11 29 0.001836
11 30 0.001564
11 31 0.000558
11 32 0.000599
11 33 0.001035
11 34 0.007481
11 35 0.004355
11 36 0.003110
11 37 0.000717
11 38 0.005118
11 39 0.000682
11 40 0.002556
11 41 0.000507
12 1 0.002013
12 2 0.018266
12 3 0.000961
12 4 0.000245
12 5 0.000471
12 6 0.006568
12 7 0.001558
12 8 0.004177
12 9 0.002128
12 10 0.000156
12 11 0.002857
12 12 0.009246
12 13 0.003179
12 14 0.012386
12 15 0.001328
12 16 0.003121
12 17 0.006393
12 18 0.003474
12 19 0.001736
12 20 0.002980
12 21 0.005016
12 22 0.000320
12 23 0.002827
12 24 0.001288
12 25 0.000238
12 26 0.000826
12 27 0.000572
12 28 0.000166
12 29 0.001885
12 30 0.000830
12 31 0.000144
12 32 0.000932
12 33 0.000425
12 34 0.003256
12 35 0.002635
12 36 0.001422
12 37 0.000447
12 38 0.002622
12 39 0.000368
12 40 0.001273
12 41 0.000636
13 1 0.007807
13 2 0.005102
13 3 0.004810
13 4 0.000464
13 5 0.000661
13 6 0.000373
13 7 0.001032
13 8 0.006997
13 9 0.001445
13 10 0.000518
13 11 0.002101
13 12 0.003179
13 13 0.002080
13 14 0.013261
13 15 0.000578
13 16 0.001908
13 17 0.004670
13 18 0.000527
13 19 0.000229
13 20 0.000833
13 21 0.002396
13 22 0.000774
13 23 0.004272
13 24 0.000347
13 25 0.001156
13 26 0.002385
13 27 0.000183
13 28 0.001071
13 29 0.000117
13 30 0.000092
13 31 0.000691
13 32 0.000052
13 33 0.000081
13 34 0.001271
13 35 0.000268
13 36 0.000322
13 37 0.000037
13 38 0.000385
13 39 0.000053
13 40 0.000249
13 41 0.000081
14 1 0.004710
14 2 0.004587
14 3 0.002360
14 4 0.000143
14 5 0.000171
14 6 0.002868
14 7 0.001463
14 8 0.001531
14 9 0.001135
14 10 0.000300
14 11 0.000525
14 12 0.012386
14 13 0.013261
14 14 0.001583
14 15 0.000754
14 16 0.000688
14 17 0.000435
14 18 0.002026
14 19 0.002313
14 20 0.001903
14 21 0.000458
14 22 0.000805
14 23 0.000483
14 24 0.002539
14 25 0.002020
14 26 0.000669
14 27 0.001872
14 28 0.001261
14 29 0.001119
14 30 0.000916
14 31 0.000165
14 32 0.001413
14 33 0.000869
14 34 0.008442
14 35 0.005372
14 36 0.003560
14 37 0.000914
14 38 0.006377
14 39 0.000829
14 40 0.003166
14 41 0.001169
15 1 0.000738
15 2 0.001566
15 3 0.000482
15 4 0.000146
15 5 0.000136
15 6 0.000706
15 7 0.001487
15 8 0.000965
15 9 0.000644
15 10 0.000487
15 11 0.000788
15 12 0.001328
15 13 0.000578
15 14 0.000754
15 15 0.001295
15 16 0.000466
15 17 0.000463
15 18 0.000243
15 19 0.000168
15 20 0.000304
15 21 0.000298
15 22 0.000227
15 23 0.000285
15 24 0.000081
15 25 0.000072
15 26 0.000087
15 27 0.000069
15 28 0.000055
15 29 0.000134
15 30 0.000102
15 31 0.000030
15 32 0.000082
15 33 0.000031
15 34 0.000713
15 35 0.000206
15 36 0.000122
15 37 0.000053
15 38 0.000058
15 39 0.000020
15 40 0.000115
15 41 0.000016
16 1 0.001086
16 2 0.006999
16 3 0.001844
16 4 0.000259
16 5 0.000193
16 6 0.004563
16 7 0.000725
16 8 0.000287
16 9 0.000349
16 10 0.000090
16 11 0.000519
16 12 0.003121
16 13 0.001908
16 14 0.000688
16 15 0.000466
16 16 0.000667
16 17 0.000552
16 18 0.002635
16 19 0.001162
16 20 0.000903
16 21 0.001129
16 22 0.000126
16 23 0.000180
16 24 0.000649
16 25 0.000467
16 26 0.000054
16 27 0.000468
16 28 0.000644
16 29 0.001014
16 30 0.000686
16 31 0.000254
16 32 0.000951
16 33 0.000388
16 34 0.003059
16 35 0.002034
16 36 0.001259
16 37 0.000337
16 38 0.002289
16 39 0.000311
16 40 0.001136
16 41 0.000427
17 1 0.002309
17 2 0.003142
17 3 0.001643
17 4 0.000153
17 5 0.000077
17 6 0.002418
17 7 0.000548
17 8 0.000556
17 9 0.000338
17 10 0.000095
17 11 0.000324
17 12 0.006393
17 13 0.004670
17 14 0.000435
17 15 0.000463
17 16 0.000552
17 17 0.000605
17 18 0.002080
17 19 0.002295
17 20 0.001422
17 21 0.000711
17 22 0.000313
17 23 0.000201
17 24 0.001051
17 25 0.000863
17 26 0.000271
17 27 0.000797
17 28 0.000675
17 29 0.000811
17 30 0.000605
17 31 0.000145
17 32 0.001444
17 33 0.000469
17 34 0.004281
17 35 0.002653
17 36 0.001704
17 37 0.000442
17 38 0.003075
17 39 0.000406
17 40 0.001545
17 41 0.000533
18 1 0.000526
18 2 0.003955
18 3 0.000353
18 4 0.000047
18 5 0.000319
18 6 0.001436
18 7 0.000181
18 8 0.000648
18 9 0.001760
18 10 0.000143
18 11 0.001429
18 12 0.003474
18 13 0.000527
18 14 0.002026
18 15 0.000243
18 16 0.002635
18 17 0.002080
18 18 0.002062
18 19 0.000824
18 20 0.002511
18 21 0.001605
18 22 0.000085
18 23 0.000632
18 24 0.000216
18 25 0.000027
18 26 0.000210
18 27 0.000042
18 28 0.000023
18 29 0.000482
18 30 0.000284
18 31 0.000087
18 32 0.000867
18 33 0.000184
18 34 0.000827
18 35 0.000755
18 36 0.000398
18 37 0.000136
18 38 0.000777
18 39 0.000104
18 40 0.000372
18 41 0.000068
19 1 0.000717
19 2 0.003467
19 3 0.000337
19 4 0.000030
19 5 0.000205
19 6 0.000943
19 7 0.000204
19 8 0.000809
19 9 0.000886
19 10 0.000045
19 11 0.000813
19 12 0.001736
19 13 0.000229
19 14 0.002313
19 15 0.000168
19 16 0.001162
19 17 0.002295
19 18 0.000824
19 19 0.001585
19 20 0.001231
19 21 0.001653
19 22 0.000063
19 23 0.000608
19 24 0.000133
19 25 0.000037
19 26 0.000250
19 27 0.000030
19 28 0.000029
19 29 0.000272
19 30 0.000115
19 31 0.000071
19 32 0.000514
19 33 0.000058
19 34 0.000326
19 35 0.000339
19 36 0.000165
19 37 0.000060
19 38 0.000324
19 39 0.000045
19 40 0.000153
19 41 0.000060
20 1 0.000225
20 2 0.006782
20 3 0.000266
20 4 0.000132
20 5 0.000093
20 6 0.003271
20 7 0.000436
20 8 0.000467
20 9 0.000424
20 10 0.000109
20 11 0.000771
20 12 0.002980
20 13 0.000833
20 14 0.001903
20 15 0.000304
20 16 0.000903
20 17 0.001422
20 18 0.002511
20 19 0.001231
20 20 0.002778
20 21 0.002326
20 22 0.000042
20 23 0.000476
20 24 0.000379
20 25 0.000070
20 26 0.000094
20 27 0.000153
20 28 0.000132
20 29 0.000801
20 30 0.000486
20 31 0.000027
20 32 0.002739
20 33 0.000248
20 34 0.001273
20 35 0.001108
20 36 0.000606
20 37 0.000190
20 38 0.001166
20 39 0.000164
20 40 0.000548
20 41 0.000207
21 1 0.000402
21 2 0.003863
21 3 0.000340
21 4 0.000059
21 5 0.000125
21 6 0.001964
21 7 0.000089
21 8 0.000422
21 9 0.000831
21 10 0.000008
21 11 0.000469
21 12 0.005016
21 13 0.002396
21 14 0.000458
21 15 0.000298
21 16 0.001129
21 17 0.000711
21 18 0.001605
21 19 0.001653
21 20 0.002326
21 21 0.001530
21 22 0.000067
21 23 0.000142
21 24 0.000663
21 25 0.000223
21 26 0.000023
21 27 0.000373
21 28 0.000209
21 29 0.000670
21 30 0.000428
21 31 0.000021
21 32 0.001774
21 33 0.000317
21 34 0.002060
21 35 0.001570
21 36 0.000922
21 37 0.000272
21 38 0.001748
21 39 0.000238
21 40 0.000838
21 41 0.000285
22 1 0.002900
22 2 0.000339
22 3 0.002268
22 4 0.000509
22 5 0.000140
22 6 0.000990
22 7 0.000126
22 8 0.000738
22 9 0.000141
22 10 0.000470
22 11 0.000196
22 12 0.000320
22 13 0.000774
22 14 0.000805
22 15 0.000227
22 16 0.000126
22 17 0.000313
22 18 0.000085
22 19 0.000063
22 20 0.000042
22 21 0.000067
22 22 0.001062
22 23 0.000730
22 24 0.000282
22 25 0.001030
22 26 0.000595
22 27 0.000198
22 28 0.000552
22 29 0.000185
22 30 0.000379
22 31 0.000210
22 32 0.000103
22 33 0.000236
22 34 0.001420
22 35 0.000751
22 36 0.000630
22 37 0.000103
22 38 0.000917
22 39 0.000145
22 40 0.000432
22 41 0.000194
23 1 0.001914
23 2 0.001500
23 3 0.001444
23 4 0.000192
23 5 0.000068
23 6 0.001485
23 7 0.000234
23 8 0.000700
23 9 0.000207
23 10 0.000058
23 11 0.000330
23 12 0.002827
23 13 0.004272
23 14 0.000483
23 15 0.000285
23 16 0.000180
23 17 0.000201
23 18 0.000632
23 19 0.000608
23 20 0.000476
23 21 0.000142
23 22 0.000730
23 23 0.001068
23 24 0.001550
23 25 0.001930
23 26 0.000897
23 27 0.000859
23 28 0.000655
23 29 0.000454
23 30 0.000486
23 31 0.000140
23 32 0.000425
23 33 0.000399
23 34 0.003526
23 35 0.002187
23 36 0.001504
23 37 0.000342
23 38 0.002582
23 39 0.000358
23 40 0.001267
23 41 0.000665
24 1 0.001965
24 2 0.001791
24 3 0.001087
24 4 0.000068
24 5 0.000207
24 6 0.000222
24 7 0.000118
24 8 0.001337
24 9 0.000647
24 10 0.000049
24 11 0.000848
24 12 0.001288
24 13 0.000347
24 14 0.002539
24 15 0.000081
24 16 0.000649
24 17 0.001051
24 18 0.000216
24 19 0.000133
24 20 0.000379
24 21 0.000663
24 22 0.000282
24 23 0.001550
24 24 0.000512
24 25 0.000325
24 26 0.000950
24 27 0.000148
24 28 0.000205
24 29 0.000054
24 30 0.000010
24 31 0.000181
24 32 0.000034
24 33 0.000004
24 34 0.000138
24 35 0.000026
24 36 0.000034
24 37 0.000004
24 38 0.000036
24 39 0.000005
24 40 0.000025
24 41 0.000081
25 1 0.005086
25 2 0.000252
25 3 0.003963
25 4 0.000219
25 5 0.000337
25 6 0.000473
25 7 0.000049
25 8 0.001438
25 9 0.000847
25 10 0.000095
25 11 0.001295
25 12 0.000238
25 13 0.001156
25 14 0.002020
25 15 0.000072
25 16 0.000467
25 17 0.000863
25 18 0.000027
25 19 0.000037
25 20 0.000070
25 21 0.000223
25 22 0.001030
25 23 0.001930
25 24 0.000325
25 25 0.001389
25 26 0.001357
25 27 0.000945
25 28 0.001074
25 29 0.000121
25 30 0.000248
25 31 0.000648
25 32 0.000028
25 33 0.000173
25 34 0.002172
25 35 0.000930
25 36 0.000793
25 37 0.000143
25 38 0.001292
25 39 0.000160
25 40 0.000670
25 41 0.000387
26 1 0.003628
26 2 0.000400
26 3 0.002551
26 4 0.000148
26 5 0.000066
26 6 0.000848
26 7 0.000069
26 8 0.000431
26 9 0.000069
26 10 0.000072
26 11 0.000477
26 12 0.000826
26 13 0.002385
26 14 0.000669
26 15 0.000087
26 16 0.000054
26 17 0.000271
26 18 0.000210
26 19 0.000250
26 20 0.000094
26 21 0.000023
26 22 0.000595
26 23 0.000897
26 24 0.000950
26 25 0.001357
26 26 0.001063
26 27 0.001091
26 28 0.000863
26 29 0.000255
26 30 0.000332
26 31 0.000333
26 32 0.000174
26 33 0.000272
26 34 0.002554
26 35 0.001408
26 36 0.001027
26 37 0.000224
26 38 0.001793
26 39 0.000237
26 40 0.000892
26 41 0.000828
27 1 0.003113
27 2 0.000605
27 3 0.002380
27 4 0.000228
27 5 0.000279
27 6 0.000143
27 7 0.000045
27 8 0.001434
27 9 0.000611
27 10 0.000138
27 11 0.000567
27 12 0.000572
27 13 0.000183
27 14 0.001872
27 15 0.000069
27 16 0.000468
27 17 0.000797
27 18 0.000042
27 19 0.000030
27 20 0.000153
27 21 0.000373
27 22 0.000198
27 23 0.000859
27 24 0.000148
27 25 0.000945
27 26 0.001091
27 27 0.000698
27 28 0.000528
27 29 0.000020
27 30 0.000120
27 31 0.000333
27 32 0.000007
27 33 0.000080
27 34 0.000537
27 35 0.000181
27 36 0.000181
27 37 0.000027
27 38 0.000278
27 39 0.000034
27 40 0.000149
27 41 0.000673
28 1 0.004637
28 2 0.000456
28 3 0.004403
28 4 0.000371
28 5 0.001337
28 6 0.000346
28 7 0.000075
28 8 0.000838
28 9 0.001476
28 10 0.000234
28 11 0.001974
28 12 0.000166
28 13 0.001071
28 14 0.001261
28 15 0.000055
28 16 0.000644
28 17 0.000675
28 18 0.000023
28 19 0.000029
28 20 0.000132
28 21 0.000209
28 22 0.000552
28 23 0.000655
28 24 0.000205
28 25 0.001074
28 26 0.000863
28 27 0.000528
28 28 0.000844
28 29 0.000108
28 30 0.000263
28 31 0.000904
28 32 0.000008
28 33 0.000151
28 34 0.001495
28 35 0.000593
28 36 0.000531
28 37 0.000090
28 38 0.000841
28 39 0.000105
28 40 0.000440
28 41 0.000232
29 1 0.001013
29 2 0.002923
29 3 0.000950
29 4 0.000373
29 5 0.000827
29 6 0.001395
29 7 0.000051
29 8 0.000587
29 9 0.001795
29 10 0.000288
29 11 0.001836
29 12 0.001885
29 13 0.000117
29 14 0.001119
29 15 0.000134
29 16 0.001014
29 17 0.000811
29 18 0.000482
29 19 0.000272
29 20 0.000801
29 21 0.000670
29 22 0.000185
29 23 0.000454
29 24 0.000054
29 25 0.000121
29 26 0.000255
29 27 0.000020
29 28 0.000108
29 29 0.000296
29 30 0.000156
29 31 0.000439
29 32 0.000199
29 33 0.000096
29 34 0.000096
29 35 0.000174
29 36 0.000067
29 37 0.000031
29 38 0.000137
29 39 0.000025
29 40 0.000057
29 41 0.000003
30 1 0.001535
30 2 0.001930
30 3 0.001103
30 4 0.000470
30 5 0.000396
30 6 0.000931
30 7 0.000077
30 8 0.000284
30 9 0.001184
30 10 0.000628
30 11 0.001564
30 12 0.000830
30 13 0.000092
30 14 0.000916
30 15 0.000102
30 16 0.000686
30 17 0.000605
30 18 0.000284
30 19 0.000115
30 20 0.000486
30 21 0.000428
30 22 0.000379
30 23 0.000486
30 24 0.000010
30 25 0.000248
30 26 0.000332
30 27 0.000120
30 28 0.000263
30 29 0.000156
30 30 0.000305
30 31 0.000376
30 32 0.000119
30 33 0.000130
30 34 0.000057
30 35 0.000088
30 36 0.000041
30 37 0.000017
30 38 0.000065
30 39 0.000011
30 40 0.000029
30 41 0.000027
31 1 0.002308
31 2 0.000230
31 3 0.002892
31 4 0.000256
31 5 0.000872
31 6 0.000913
31 7 0.000060
31 8 0.000341
31 9 0.000762
31 10 0.000053
31 11 0.000558
31 12 0.000144
31 13 0.000691
31 14 0.000165
31 15 0.000030
31 16 0.000254
31 17 0.000145
31 18 0.000087
31 19 0.000071
31 20 0.000027
31 21 0.000021
31 22 0.000210
31 23 0.000140
31 24 0.000181
31 25 0.000648
31 26 0.000333
31 27 0.000333
31 28 0.000904
31 29 0.000439
31 30 0.000376
31 31 0.000718
31 32 0.000022
31 33 0.000252
31 34 0.001284
31 35 0.000637
31 36 0.000506
31 37 0.000097
31 38 0.000840
31 39 0.000109
31 40 0.000424
31 41 0.000211
32 1 0.000461
32 2 0.002313
32 3 0.000116
32 4 0.000045
32 5 0.000080
32 6 0.000871
32 7 0.000184
32 8 0.000296
32 9 0.000380
32 10 0.000125
32 11 0.000599
32 12 0.000932
32 13 0.000052
32 14 0.001413
32 15 0.000082
32 16 0.000951
32 17 0.001444
32 18 0.000867
32 19 0.000514
32 20 0.002739
32 21 0.001774
32 22 0.000103
32 23 0.000425
32 24 0.000034
32 25 0.000028
32 26 0.000174
32 27 0.000007
32 28 0.000008
32 29 0.000199
32 30 0.000119
32 31 0.000022
32 32 0.001953
32 33 0.000050
32 34 0.000130
32 35 0.000174
32 36 0.000079
32 37 0.000031
32 38 0.000158
32 39 0.000023
32 40 0.000071
32 41 0.000015
33 1 0.001084
33 2 0.001273
33 3 0.000621
33 4 0.000143
33 5 0.000189
33 6 0.000526
33 7 0.000100
33 8 0.000247
33 9 0.000606
33 10 0.000302
33 11 0.001035
33 12 0.000425
33 13 0.000081
33 14 0.000869
33 15 0.000031
33 16 0.000388
33 17 0.000469
33 18 0.000184
33 19 0.000058
33 20 0.000248
33 21 0.000317
33 22 0.000236
33 23 0.000399
33 24 0.000004
33 25 0.000173
33 26 0.000272
33 27 0.000080
33 28 0.000151
33 29 0.000096
33 30 0.000130
33 31 0.000252
33 32 0.000050
33 33 0.000066
33 34 0.000013
33 35 0.000016
33 36 0.000006
33 37 0.000003
33 38 0.000004
33 39 0.000001
33 40 0.000002
33 41 0.000013
34 1 0.012962
34 2 0.006755
34 3 0.008839
34 4 0.000298
34 5 0.001395
34 6 0.001106
34 7 0.000632
34 8 0.004533
34 9 0.004843
34 10 0.000958
34 11 0.007481
34 12 0.003256
34 13 0.001271
34 14 0.008442
34 15 0.000713
34 16 0.003059
34 17 0.004281
34 18 0.000827
34 19 0.000326
34 20 0.001273
34 21 0.002060
34 22 0.001420
34 23 0.003526
34 24 0.000138
34 25 0.002172
34 26 0.002554
34 27 0.000537
34 28 0.001495
34 29 0.000096
34 30 0.000057
34 31 0.001284
34 32 0.000130
34 33 0.000013
34 34 0.001267
34 35 0.000525
34 36 0.000432
34 37 0.000048
34 38 0.000463
34 39 0.000129
34 40 0.000390
34 41 0.000152
35 1 0.006265
35 2 0.005267
35 3 0.004043
35 4 0.000200
35 5 0.000837
35 6 0.001049
35 7 0.000599
35 8 0.002684
35 9 0.002952
35 10 0.000509
35 11 0.004355
35 12 0.002635
35 13 0.000268
35 14 0.005372
35 15 0.000206
35 16 0.002034
35 17 0.002653
35 18 0.000755
35 19 0.000339
35 20 0.001108
35 21 0.001570
35 22 0.000751
35 23 0.002187
35 24 0.000026
35 25 0.000930
35 26 0.001408
35 27 0.000181
35 28 0.000593
35 29 0.000174
35 30 0.000088
35 31 0.000637
35 32 0.000174
35 33 0.000016
35 34 0.000525
35 35 0.000130
35 36 0.000125
35 37 0.000057
35 38 0.000045
35 39 0.000039
35 40 0.000097
35 41 0.000026
36 1 0.004986
36 2 0.002998
36 3 0.003364
36 4 0.000197
36 5 0.000594
36 6 0.000515
36 7 0.000353
36 8 0.001953
36 9 0.001986
36 10 0.000398
36 11 0.003110
36 12 0.001422
36 13 0.000322
36 14 0.003560
36 15 0.000122
36 16 0.001259
36 17 0.001704
36 18 0.000398
36 19 0.000165
36 20 0.000606
36 21 0.000922
36 22 0.000630
36 23 0.001504
36 24 0.000034
36 25 0.000793
36 26 0.001027
36 27 0.000181
36 28 0.000531
36 29 0.000067
36 30 0.000041
36 31 0.000506
36 32 0.000079
36 33 0.000006
36 34 0.000432
36 35 0.000125
36 36 0.000170
36 37 0.000054
36 38 0.000085
36 39 0.000027
36 40 0.000141
36 41 0.000042
37 1 0.000967
37 2 0.000906
37 3 0.000612
37 4 0.000017
37 5 0.000127
37 6 0.000183
37 7 0.000077
37 8 0.000423
37 9 0.000501
37 10 0.000099
37 11 0.000717
37 12 0.000447
37 13 0.000037
37 14 0.000914
37 15 0.000053
37 16 0.000337
37 17 0.000442
37 18 0.000136
37 19 0.000060
37 20 0.000190
37 21 0.000272
37 22 0.000103
37 23 0.000342
37 24 0.000004
37 25 0.000143
37 26 0.000224
37 27 0.000027
37 28 0.000090
37 29 0.000031
37 30 0.000017
37 31 0.000097
37 32 0.000031
37 33 0.000003
37 34 0.000048
37 35 0.000057
37 36 0.000054
37 37 0.000054
37 38 0.000016
37 39 0.000011
37 40 0.000021
37 41 0.000004
38 1 0.008079
38 2 0.005563
38 3 0.005295
38 4 0.000193
38 5 0.000980
38 6 0.000922
38 7 0.000366
38 8 0.003066
38 9 0.003506
38 10 0.000560
38 11 0.005118
38 12 0.002622
38 13 0.000385
38 14 0.006377
38 15 0.000058
38 16 0.002289
38 17 0.003075
38 18 0.000777
38 19 0.000324
38 20 0.001166
38 21 0.001748
38 22 0.000917
38 23 0.002582
38 24 0.000036
38 25 0.001292
38 26 0.001793
38 27 0.000278
38 28 0.000841
38 29 0.000137
38 30 0.000065
38 31 0.000840
38 32 0.000158
38 33 0.000004
38 34 0.000463
38 35 0.000045
38 36 0.000085
38 37 0.000016
38 38 0.000143
38 39 0.000031
38 40 0.000142
38 41 0.000055
39 1 0.001031
39 2 0.000758
39 3 0.000677
39 4 0.000046
39 5 0.000136
39 6 0.000145
39 7 0.000061
39 8 0.000416
39 9 0.000456
39 10 0.000079
39 11 0.000682
39 12 0.000368
39 13 0.000053
39 14 0.000829
39 15 0.000020
39 16 0.000311
39 17 0.000406
39 18 0.000104
39 19 0.000045
39 20 0.000164
39 21 0.000238
39 22 0.000145
39 23 0.000358
39 24 0.000005
39 25 0.000160
39 26 0.000237
39 27 0.000034
39 28 0.000105
39 29 0.000025
39 30 0.000011
39 31 0.000109
39 32 0.000023
39 33 0.000001
39 34 0.000129
39 35 0.000039
39 36 0.000027
39 37 0.000011
39 38 0.000031
39 39 0.000075
39 40 0.000037
39 41 0.000006
40 1 0.004152
40 2 0.002707
40 3 0.002746
40 4 0.000074
40 5 0.000495
40 6 0.000455
40 7 0.000216
40 8 0.001524
40 9 0.001763
40 10 0.000294
40 11 0.002556
40 12 0.001273
40 13 0.000249
40 14 0.003166
40 15 0.000115
40 16 0.001136
40 17 0.001545
40 18 0.000372
40 19 0.000153
40 20 0.000548
40 21 0.000838
40 22 0.000432
40 23 0.001267
40 24 0.000025
40 25 0.000670
40 26 0.000892
40 27 0.000149
40 28 0.000440
40 29 0.000057
40 30 0.000029
40 31 0.000424
40 32 0.000071
40 33 0.000002
40 34 0.000390
40 35 0.000097
40 36 0.000141
40 37 0.000021
40 38 0.000142
40 39 0.000037
40 40 0.000273
40 41 0.000033
41 1 0.001417
41 2 0.000603
41 3 0.001203
41 4 0.000093
41 5 0.000228
41 6 0.000027
41 7 0.000008
41 8 0.000850
41 9 0.000634
41 10 0.000027
41 11 0.000507
41 12 0.000636
41 13 0.000081
41 14 0.001169
41 15 0.000016
41 16 0.000427
41 17 0.000533
41 18 0.000068
41 19 0.000060
41 20 0.000207
41 21 0.000285
41 22 0.000194
41 23 0.000665
41 24 0.000081
41 25 0.000387
41 26 0.000828
41 27 0.000673
41 28 0.000232
41 29 0.000003
41 30 0.000027
41 31 0.000211
41 32 0.000015
41 33 0.000013
41 34 0.000152
41 35 0.000026
41 36 0.000042
41 37 0.000004
41 38 0.000055
41 39 0.000006
41 40 0.000033
41 41 0.000508
#5Re:Multiwfn and wavefunction analysis»How do we calculate the local excitation and charge transfer ?»2021-10-26 05:59:06
Thank you very much. After a detailed questions my all the questions have been cleared and I have learned alot from your detailed answers. I can say this forum is really a great opportunity for all of us Multiwfn users. I have asked you many questions and you have responded all the answers in very humble way. Thank you soo much.
#6Re:Multiwfn and wavefunction analysis»How do we calculate the local excitation and charge transfer ?»2021-10-25 06:26:11
You statement is a bit too complicated and somewhat confused me. I would like to clarify a few key points:
(1)TDDFT calculation is performed based on ground state wavefunction, which is known as reference state. For a specific geometric structure, the S1, S2, T1, T2 ... excited states calculated by TDDFT are represented based on the same set of orbitals, namely ground state MOs, but their configuration coefficients are different. Assume that ground state electronic state is S0, then in IFCT analysis, if in the current case Exc. 2 corresponds to S2 and you selected it, then IFCT analysis will be performed for S0-S2 excitation.
(2)At different geometries, the ground state MOs are different. Hence, if you optimized S0, S1, S2 states... respectively, you will find the MOs recorded in the .fch files generated by these calculations are different. If two geometries differ with each other marginally, then their MOs should have very similar characters.
(3)IFCT can only be used to characterize vertical transition, it cannot be used for studying adiabatic transition. For example, you can use IFCT to analyze S0-S1 transition at S0 geometry, and you can also analyze S0-S1 excitation at S1 or other geometies, this depends on your practical purpose. For example, if you are interested in vertical absorption from S0 to S2 state at geometry of ground state S0, you should perform TDDFT calcluation at optimized S0 geometry, then in the IFCT analysis select "Exc. 2". Another example, if you want to characterize S1-S0 vertical emission at S1 geometry, you should optimized S1 first, then select "Exc. 1" in the IFCT analysis interface.
Using HOMO and LUMO to discuss transition character is highly deprecated. Since it is very rare that an electron excitation is fully dominated by HOMO-LUMO transition. Sometimes, even the lowest electron excitation may solely contributed to transition between other MOs, for example I found S0-S1 excitation of azobenzene at TD-PBE0/6-31G* level almost completely corresponds to HOMO-1 to LUMO transition.
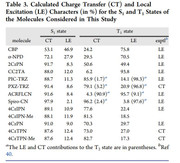
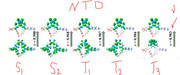
Thank you for your response. I would like to clear my statement as I have optimized the different geometries like S0, S1, S2, T1, T2 and T3. After optimizing these different geometries, I have calculated their TDDFT with TDA-wb97xd/6-31g(d,p) keywords calculations for excited energy and for configuration coefficients. I have also calculated their NTOs with TDA keywords. I want to calculate the % CT and % LE for each excited state. I have also attached the one reference paper images for your understanding in which % CT and % LE have been calculated at different excited states. I have performed both vertical (optimized S0 geometry and then use this geometry as a reference to calculate the TDDFT calculations for S1, S2, T1, T2 and T3) and adiabatic (Optimized the S1, S2, T1, T2 and T3 excited states and then used S1 optimized geometry for calculations of S1 excited state TDDFT calculations and similarly S2 optimized geometry used for S2 TDDFT Calculations, T1 optimized geometry used for T1 TDDFT calculations ........etc) calculations. This was the confusion which I am facing during % CT and % LE charcters calculations during IFCT analysis because I am just finding there only three excited states and I am confused that either in every case I will use Excited State 1 aur different but you have make it clear that excited state 2 means S0->S2. I should repeat my question as I want to calculate the % CT and % LE at different excited states and I have the optimized geometries and their TDDFT calculations with vertical and adiabatic geometries. I hope now my question is clear and you can guide me in easiest way.
The most important point as you mentioned in (3) of your answer as if I want to calculate the S1->S0, then first I need to optimized the S1 geometry and then perform the TDDFT calculations. So, its means to calculate the % CT and % LE at this state I will use the .fchk file of TDDFT calculations based on S1 optimized geometry?
Secondly, If I will use the T3 optimzed geometry and perform the TDDFT calculations, so its means it will give me emission energy of T3->S0 then I want to calculate the % CT and % LE at this state T3 and my question is that in IFCT analysis I will select the Excited state 3?
Thank you soo much for your attentions and your time.
#7Re:Multiwfn and wavefunction analysis»How do we calculate the local excitation and charge transfer ?»2021-10-25 04:25:09
Usman Ali wrote:Although, I asked four questions at the same time but I hope you should respond me in details. I am very hopeful on having this forum for clearing my confusions and to complete the analysis.
Your response should be highly respected.
Thanks
1 If you partition the whole system as two fragments in IFCT analysis, assume that sum of charge transfer of 1->2 and 2->1 is e.g. 0.8, that means %CT is 80%.
2 You should always follow the prompt on screen, the prompt in each step is very clear. I strongly suggest you to reproduce the IFCT analysis in Section 4.18.8 of Multiwfn manual, you will learn the usage and basic idea of IFCT analysis.
3 MLCT and LMCT are only defined for transition metal coordinates. For other kinds of systems these words are inappropriate. For OLED, there is no transition metal atom and ligands at all.
4 I believe there is no evident confusion.The meaning of hole and electron has already been clearly described in Section 3.21.1, and MLCT is a well recognized concept, you can find abundant introductory materials via Google. MLCT(%) simply refers to CT(%) from metal (M) to ligands (L) during a specific electronic excitation.
Thank you for your answer. I have cleared my concept about %CT and %LE chracters calculations via IFCT method. Although it is great tool for analysis. I have question about IFCT calculations at different excited excited states as I have performed the Adiabatic calculations for different excited states like S1, S2, T1, T2 and T3 for OLEDs molecules. During the IFCT calculations for % CT and % LE, the excited states on the screen is always as Exc. 1, Exc. 2 and Exc. 3. As in the case of S1 TDDFT calculations, I select the Exc. 1 state for % CT and % LE results but in the case of S2, I have selected the Exc. 2 for %CT and %LE charcters but the results are huge different from S1 and S2 %CT and %LE charcters although the pictures of HOMO and LUMO at both excited state are nearly same not a much different. So, my question is that how we can perfomed the IFCT analysis for calculating the % CT and % LE charcters for different excited states?
Either for S1, we need to pick the Exc. 1 and S2, we need to pick the Exc. 2 results and so on?
Either in all case we will select the Exc. 1 does not matter which file we load for IFCT analysis as S1, S2, T1, T2 and T3 etc because if I pick the Exc.1 in different geometries analysis like S1, S2, T1, T2 and T3 then the results are nearly same and looking acceptable when we compare these results based on their molecular HOMO and LUMO orbitals pictures. I have also attached the screens shots of my questions. I have completely share the results for your clear understanding about my querries.
Kindly respond me in this regard.
#8Re:Multiwfn and wavefunction analysis»How do we calculate the local excitation and charge transfer ?»2021-10-21 04:19:45
The percentage of CT character can be characterized in many ways by Multiwfn, for example, see this part of Section 4.18.1 of Multiwfn manual on how to quantify it according to the data given by hole-electron analysis:
https://i.postimg.cc/PPnfdFJ5/Clipboard01.png
Note that the value of CT% is closely related to the definition of fragments. The acceptor and donor may be defined as the fragments in the analysis.
In addition, you can use the IFCT (interfragment charge transfer) analysis to obtain various details of charge transfer between fragments, see Section 4.18.8 of manual for examples.
In the table you mentioned, the question mark denotes that the magnitude of the corresponding quantity is not clear, it may be small and may be large, depending on practical situation.
I have read you response on this post which is likely of my interest. I have some confusions and questions regarding CT and LE percentage calculations. My first question is as you mentioned the table in MLCT % values are given, So I want to know how I can get this table as there is no output results during using the IFCT module of Multiwfn?
My second question is what will be the next step during using the IFCT module for calcuting CT and LE% in Multiwfn as I also attached the screenshot of my querry.
My third confusion is as you used MLCT and LMCT term for your response also in manual and also in reply of this post, so in our case as we are working on OLEDs then we will use the same term for calculating the CT and LE % ?
My last confusion is as you mentioned hole (Ru%), ele (Ru%) and MLCT (%) for explanation but it creates a confusion for beginers that what is simply the CT% and what will be the LE% for our calculations?
Although, I asked four questions at the same time but I hope you should respond me in details. I am very hopeful on having this forum for clearing my confusions and to complete the analysis.
Your response should be highly respected.
Thanks
#9Re:Multiwfn and wavefunction analysis»The overlap between HONTO and LUNTO»2021-10-21 02:39:52
Thank you very much for your help. I have completed this analysis.
#10Re:Multiwfn and wavefunction analysis»The overlap between HONTO and LUNTO»2021-10-19 02:15:44
Thank you soo much. After your detail guidance, I have found the Sm index for overlap. I would like to know that Sm value is in a.u units, So it would require to chnage this value into eV units or its should be use as such. Also, tell me which units are better for its explanation as it is not mentioned in mannual. The picture I send you before for reproductions of such results not explains any unit. Kindly guide me in this regard.
Thanks
#11Re:Multiwfn and wavefunction analysis»The overlap between HONTO and LUNTO»2021-10-14 02:06:54
1 NTOs are orthogonal with each other, so it is obvious that overlap integral between two different NTOs must be an extremely small value (exactly zero, in principle). To reproduce the data in your photo, you should use hole-electron analysis module of Multiwfn and take Sm index:
https://i.postimg.cc/68FzFCXH/Clipboard01.png(screenshot of Section 3.21.1 of multiwfn manual)
See Section 4.18.1 of Multiwfn manual for example on how to use hole-electron analysis module.
2 You do not need to calculate NTO at all. In fact NTO doesn't work in many cases, it is very often to find there is no NTO pair dominates the excitation of interest. In contrast, the hole-electron analysis in Multiwfn is universal and rigorous, the overlap between hole and electron measured by Sm index can faithfully describe the overlap extent in any situation. See Section 3.21.1 of Multiwfn manual for theory of hole-electron analysis.
You can respectively optimize the S0, S1, T1 geometries, and at each geometry, perform hole-electron analysis to derive Sm index for S0-S1 and S0-T1 excitations, respectively.
Thank you very much for your answer. I can not clearly understand your mean in the last line as you said "just optimize the different geometries and at each geometry to drive the Sm index". You mean from optimized geomtries, I need to calculate their TDDFT calculations for excitations and then calculate their electron-hole overlap extent?
Secondly, you mentioned that NTO are not suitable for calculating the overlap extent so if I used the simple molecular orbitals like HOMO and LUMO for calculating the overlap extent, then even the results are very small as close to zero.
I think there is a confusion for my understanding, so could you please explain it in more details.
Thank you very much for this forum to help us.
#12Re:Multiwfn and wavefunction analysis»The overlap between HONTO and LUNTO»2021-10-13 03:13:12
Hi,
You can firstly use Multiwfn to generate NTOs (see example in Section 4.18.4), then use main function 0 to find the index corresponding to the so-called HONTO and LUNTO (the energies printed on console window now correspond to NTO eigenvalues), and then use subfunction 10 of main function 200 to evaluate overlap integral between the two orbitals.
Best regards,
Tian
Hi
After reading your reply to the this post, I have calculated the overlap of hole and electron between the HONTO and LUNTO but the answer value which I got from the Multiwfn is very different from the result like 0.00000000... something like that. I want to know should we need to multiply or accomodate this value with any factor?
Secondly, I want to ask you that I want to calculate the overlap for different states with different geometries. So, I need to calculate the NTOs via guassian calculations for every state like S1 and T1 from different geometries like S0, S1, T1, T2, T3 etc. I have also attached the figures with this question. I want to perform the calculations given in the Table S1 of the picture 2 in this post. I should be respected for your guidance and response.
Thanks
Pages:1