用NWChem做SODFT在DFT计算中考虑旋轨耦合效应

1 前言

众所周知，对重原子构成的体系，尤其是从第五周期开始（H,He算第一周期，下同），需要考虑相对论效应，否则结果可能严重错误。相对论效应分为标量和旋轨耦合两部分。标量相对论效应好考虑，用相对论赝势时即可等效体现，多数主流量化程序如Gaussian也支持标量相对论哈密顿，结合专为标量相对论计算优化的全电子基组即可（见《在赝势下做波函数分析的一些说明》 //www.umsyar.com/156）。

比较棘手的是旋轨耦合的考虑，本文只说单个态的旋轨耦合问题。最直接的考虑方式是做二分量相对论计算，但比较耗时，且支持它的ADF、Turbomole都是收费的，而免费的Dirac等程序则比较小众且功能局限性大。Gaussian里有个DKHSO方法可以在单点计算时考虑旋轨耦合效应，但是只能用于HF，因此没什么实用性。一种常用的又便宜又好的考虑旋轨耦合的做法是使用相对论赝势，但不仅要包含我们平时常用的标量势，还同时要考虑旋轨势，这种方式做DFT称为Spin-orbit DFT (SODFT)，Molpro、Turbomole、NWChem都支持。本文介绍使用其中免费的NWChem程序做SODFT的方法，并会以TlCl和HgI的解离能计算做为例子。在NWChem中，SODFT有解析梯度，因此能够容易地优化分子结构，不过Hessian只有数值的（只考虑标量势的话倒是有解析Hessian）。NWChem的SODFT还一个不足之处是没法利用对称性加速计算。

NWChem的安装方法看此文：《NWChem 6.6编译方法》（ //www.umsyar.com/270）。本文使用NWChem 6.6版。

2 SODFT计算时赝势和赝势基组的选择

赝势包括标量势、旋轨势和核极化势。标量势部分是我们最常使用的，所有相对论赝势都提供了标量势，但不是所有赝势都给出了旋轨势。给出了旋轨势的赝势比较常见的有Stuttgart赝势和CRENB赝势，对周期表覆盖得都比较全面。后者很老，精度也不比前者好，所以本文将会用前者。Stuttgart赝势也分多种，包括HF系列（赝势不体现相对论效应），WB系列（基于Wood-Boring准相对论计算的数据搞的）和DF系列（基于Dirac-Fock全相对论计算的数据搞的），我们一般都用M版（拟合赝势时考虑多个价电子），如MDF。

除赝势外还要考虑赝势基组。基于Stuttgart赝势的常用的几种选择有：
1 Stuttgart赝势的标配基组。缺点是对于大多数元素，不像下面几种给出了不同档次基组的定义，选择余地小。
2 cc-pVnZ-PP系列：结合的是Stuttgart小核MDF赝势
3 def2系列：从第五周期开始是赝势基组，结合的是Stuttgart小核赝势，对s、d、镧系元素用的是MWB，对p元素用的是MDF
4 dhf系列：和def2都是Weigend主要搞的，只定义了五、六周期的s和d族元素，p族元素和def2定义相同。此系列分为dhf和dhf-2c两种，前者主要用于做一分量计算（即常规的赝势下的计算），把def2对s、d元素用的标量势从MWB改为MDF并重新调整了赝势基组定义，由此使结果略好了一点点；后者在前者基础上增加了额外的p,d基函数，使得带着旋轨势做计算时结果更好

以上赝势基组中，做SODFT时能用dhf-2c就用dhf-2c，毕竟是给此目的专门优化的。对于本文要考察的元素，Tl、Hg、I都可以用dhf-2c，我们用其中TZVP级别的就够了，即dhf-TZVP-2c。虽然也有更好的dhf-QZVP-2c，但对于DFT计算升到QZ级别意义并不大。对于Cl，由于相对比较轻，其引起的旋轨耦合效应不会给结果带来明显影响，所以我们不对它用赝势，而对它用def2-TZVP全电子基组。

3 计算TlCl

本文我们要尝试重复下面图中的TlCl和HgI的数据，数据来自Theor. Chem. Acc., 130, 633-644 (2011)。图中BDE是键解离能，单位是kcal/mol。键解离能的计算是用解离后的原子的焓减去分子的焓。图中BDE下面的列是文中只考虑标量相对论的计算结果，BDE+SO是考虑旋轨耦合后的。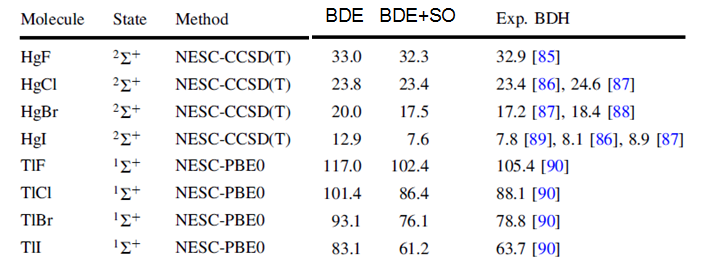

我们先算TlCl。由于文中用的是PBE0，所以我们也用PBE0，此泛函对这类体系是比较合适的。我们用的键长直接取实验值，大量双原子分子的实验平衡距离可以在NIST网站 http://webbook.nist.gov/chemistry/上很容易地查到，注意勾选Constants of diatomic molecules，之后数据页面里r_e就是平衡距离了，对此分子是2.484826埃。

首先我们得获取赝势和赝势基组定义。def2和dhf系列在Turbomole基组库 http://www.cosmologic-services.de/basis-sets/basissets.php里是最全的（EMSL上的不仅不全，而且没有旋轨势）。在此网站里面选上Tl，然后选dhf-TZVP-2c，输出格式就用默认的Turbomole（没直接提供NWChem的比较可惜）。给出的数据包括基组部分、标量势部分和旋轨势部分。
PS1：值得一提的是，当选择dhf-TZVP-2c的时候，对于非第五、六周期的元素，自动给出的是def2对应档次基组的定义
PS2：此网站输出格式里只有选Turbomole或Molpro这两种支持旋轨势的程序时输出内容才有旋轨势，我们这里不选Molpro是因为没有Turbomole的格式那么容易手动改成NWChem的格式

然后我们把Turbomole格式的基组、标量势和旋轨势的定义都改成NWChem的格式，不知道NWChem的格式怎么写就RTFM。一个较大区别是Turbomole里把收缩系数放在第一列，指数放在最后一列，和NWChem的顺序是反过来的。最终TlCl的SODFT任务的输入文件如下

start
PRINT low
geometry noautosym
Tl 0.00000 0.00000 0.00000
Cl 0.00000 0.00000 2.484826
end
basis "ao basis" spherical
Cl library def2-TZVP
Tl s
729.65038145 0.13672829828E-03
46.665548707 0.60443439951E-02
20.970448726 -0.20022066697
14.149588677 0.40801678488
Tl s
20.730134285 -0.71861135918E-01
6.1527631309 0.98057508445
Tl s
1.5757324480 1.0000000000
Tl s
0.74980169458 1.0000000000
Tl s
0.19536816194 1.0000000000
Tl s
0.70878767298E-01 1.0000000000
Tl p
15.383852616 0.61717949180
14.814929544 -0.72859235151
6.7261253658 0.40438195364
Tl p
1.9626182149 0.43157661160
1.0331857851 0.39230403853
0.53837445996 0.14007406820
Tl p
0.24446611676 1.0000000000
Tl p
0.90785377260E-01 1.0000000000
Tl p
0.33401321498E-01 1.0000000000
Tl d
57.606819928 0.16054811114E-03
9.7368866667 0.24456562496E-01
6.9256201679 -0.69914775031E-01
2.1396230731 0.19496269490
1.0836187110 0.29731629705
0.52356298209 0.23728708102
Tl d
0.23842309375 1.0000000000
Tl d
0.95000000000E-01 1.0000000000
Tl f
0.28435 1.0000000000
Tl f
0.95 1.0000000000
Tl p
32.0 -0.0005
16.0 -1.0
Tl p
8.0 -1.0125
4.0 0.7450
Tl p
2.0 1.0
Tl d
3.0 1.0
END
ECP
Tl nelec 60
Tl ul
2 1.00000000 0.00000000
Tl s
2 12.16780500 281.28466300
2 8.29490900 62.43425100
Tl p
2 7.15149200 4.63340800
2 5.17286500 9.34175600
2 9.89107200 72.29925300
2 9.00339100 144.55803700
Tl d
2 7.13021800 35.94303900
2 6.92690600 53.90959300
2 5.41757000 10.38193900
2 5.13868100 15.58382200
Tl f
2 5.62639900 15.82548800
2 5.54895200 21.10402100
2 2.87494600 2.91512700
2 2.82145100 3.89690300
Tl g
2 6.67905700 -7.49453400
2 6.70683500 -9.54057500
2 7.20928400 -7.79799200
2 7.07096400 -9.25952400
END
SO
Tl p
2 7.151492 -9.266817
2 5.172865 9.341756
2 9.891072 -144.598506
2 9.003391 144.558037
Tl d
2 7.130218 -35.943039
2 6.926906 35.939729
2 5.417570 -10.381939
2 5.138681 10.389215
Tl f
2 5.626399 -10.550326
2 5.548952 10.552010
2 2.874946 -1.943418
2 2.821451 1.948451
Tl g
2 6.679057 3.747267
2 6.706835 -3.816230
2 7.209284 3.898996
2 7.070964 -3.703809
END
dft
xc pbe0
end
task sodft

输入文件还是很容易理解的，照常定义基组部分，ECP段落指定标量势部分，SO字段指定旋轨势部分，最后task里写上SODFT就行了。noautosym写不写无所谓，由于SODFT不支持对称性，不写它时程序也不会利用对称性来加速。

然后我们运行此任务，输出文件里这部分即是SODFT能量：
Total DFT energy = -632.863447528456
在笔者的Intel 4核i7-2630QM机子下，做这个计算耗时是20.8s，若只考虑标量势是10.8s，可见考虑旋轨势还是会增加不少耗时，不过一般完全承受得起，总比做二分量相对论计算来考虑旋轨耦合效应便宜得多。

之后我们把TlCl的文件分别改写为Tl和Cl的文件，二者都是二重态，所以在dft字段里面要写上mult 2。算出的结果是Tl=-172.724034492809，Cl=-459.997396831618。因此基于单点能算的键解离能是627.51*(-459.997396831618-172.724034492809+632.863447528456)=89.116 kcal/mol。

到此还没完，我们还得计算焓的热校正量对解离能的修正。我们就不用SODFT算频率了，就直接在Gaussian里用# PBE1PBE/def2TZVP opt freq scale=0.982关键词对TlCl优化和做振动分析就完了，这里0.982是ZPE校正因子（为了省事我们不单独考虑升温对焓影响那部分的校正因子）。实际上我们查不到PBE0/def2-TZVP级别的校正因子，但由于J. Phys. Chem. A, 111, 11683 (2007)中给出PBE0结合6-311+G(2df,p)这样不错级别基组的校正因子是0.9824，所以有理由认为0.982对于PBE0结合def2-TZVP是基本合适的。计算后得到的焓的热校正量输出为
Thermal correction to Enthalpy= 0.004388
对于Tl和Cl没必要做振动分析，因为单个原子只有平动对焓有贡献，且是精确已知的，即5/2*RT，常温下对应0.002360 Hartree。所以常温下焓的热校正量对TlCl键解离能的贡献可以计算为627.51*(0.002360+0.002360-0.004388)=0.208 kcal/mol。

最后，得到TlCl的常温下键解离能是89.116+0.208=89.324 kcal/mol，这和前面贴出来的实验值88.1 kcal/mol相符极好！（对普通DFT泛函来说能达到1kcal/mol程度误差着实难能可贵）

4 计算HgI

HgI是二重态，解离后会生成单重态的Hg和二重态的I。HgI的键长在NIST上查不到，虽然某些文献里估计能查到，但这里不深究，就直接用PBE0/def2-TZVP级别来优化键长，之后再做单点计算。优化后键长是2.75663埃。（当然，若要求更精确，可以直接用SODFT优化。笔者也试了下，i7-2630QM上耗时336s，结果是2.76379埃。可见对此体系是否考虑旋轨耦合对结构影响很小，对TlCl测试过也是如此）。

我们使用上一节的方式，获取Hg和I的dhf-TZVP-2c赝势基组定义以及对应的标量势和旋轨势，写成HgI的PBE0的SODFT任务的单点输入文件，如下所示：

start
PRINT low
geometry noautosym
Hg 0.00000 0.00000 0.00000
I 0.00000 0.00000 2.75663
end
basis "ao basis" spherical
I s
5899.5791533 0.24188269271E-03
898.54238765 0.15474041742E-02
200.37237912 0.42836684457E-02
31.418053840 -0.39417936275E-01
15.645987838 0.96086691992
I s
11.815741857 0.57815778954
6.4614458287 0.37374293124
I s
2.3838067579 1.0000000000
I s
1.1712089662 1.0000000000
I s
0.32115875757 1.0000000000
I s
0.12387919364 1.0000000000
I p
185.43362455 0.83127824000E-03
20.091408146 0.63991653000E-01
9.7577022390 -0.27791138000
I p
13.068307912 -0.49793790382E-01
3.5818714205 0.38212490511
2.0282441852 0.70447564804
1.0181492146 0.33781067803
I p
0.46673773115 1.0000000000
I p
0.19242597960 1.0000000000
I p
0.74508878495E-01 1.0000000000
I d
124.20341062 0.65671747209E-03
34.587311801 0.51648185674E-02
12.767328064 -0.19881371307E-01
4.7745100133 0.21386794109
2.4582209028 0.43405444707
1.1923708147 0.37850637882
I d
0.52883971906 1.0000000000
I d
0.17008164307 1.0000000000
I f
0.44141808 1.00000000
I f
2.18 1.0000000000
I p
12.0 -0.3
6.0 1.0
I d
2.0 1.0
Hg s
48.013786990 0.58613168385E-02
21.239875095 -0.17590367988
15.876100879 0.35780354753
Hg s
5.4837607070 1.0000000000
Hg s
1.5480592128 1.0000000000
Hg s
0.72425230437 1.0000000000
Hg s
0.16369906863 1.0000000000
Hg s
0.57211615334E-01 1.0000000000
Hg p
23.291760168 -0.83564430982E-02
13.028969569 0.83703058587E-01
6.5100040792 -0.31023833705
Hg p
1.8167935815 1.0000000000
Hg p
0.90079391013 1.0000000000
Hg p
0.41304090835 1.0000000000
Hg p
0.11845879331 1.0000000000
Hg p
0.36084184656E-01 1.0000000000
Hg d
15.176302343 0.60654575178E-02
6.7004896493 -0.59880306300E-01
1.9144256118 0.31411145584
0.88641552102 0.45081091161
Hg d
0.38364767725 1.0000000000
Hg d
0.14936891490 1.0000000000
Hg f
0.79569 1.0
Hg p
19.3582 0.0635
8.7992 -0.4607
Hg p
3.9996 0.8853
Hg d
2.7000000000 1.0000000000
END
ECP
I nelec 28
I ul
2 1.000000 0.000000
I s
2 40.033376 49.989649
2 17.300576 281.006556
2 8.851720 61.416739
I p
2 15.720141 67.416239
2 15.208222 134.807696
2 8.294186 14.566548
2 7.753949 28.968422
I d
2 13.817751 35.538756
2 13.587805 53.339759
2 6.947630 9.716466
2 6.960099 14.977500
I f
2 18.522950 -20.176618
2 18.251035 -26.088077
2 7.557901 -0.220434
2 7.597404 -0.221646
Hg nelec 60
Hg ul
2 1.0000000 0.0000000
Hg s
2 12.4130710 275.7747970
2 6.8979130 49.2678980
Hg p
2 11.3103200 80.5069840
2 10.2107730 161.0348240
2 5.9398040 9.0834160
2 5.0197550 18.3677730
Hg d
2 8.4078950 51.1372560
2 8.2140860 76.7074590
2 4.0126120 6.5618210
2 3.7953980 9.8180700
Hg f
2 3.2731060 9.4290010
2 3.2083210 12.4948560
Hg g
2 4.4852960 -6.3384140
2 4.5132000 -8.0998630
END
SO
I p
2 15.720141 -134.832478
2 15.208222 134.807696
2 8.294186 -29.133096
2 7.753949 28.968422
I d
2 13.817751 -35.538756
2 13.587805 35.559839
2 6.947630 -9.716466
2 6.960099 9.985000
I f
2 18.522950 13.451079
2 18.251035 -13.044039
2 7.557901 0.146956
2 7.597404 -0.110823
Hg p
2 11.31032000 -161.01396700
2 10.21077300 161.03482400
2 5.93980400 -18.16683200
2 5.01975500 18.36777300
Hg d
2 8.40789500 -51.13725600
2 8.21408600 51.13830600
2 4.01261200 -6.56182100
2 3.79539800 6.54538000
Hg f
2 3.27310600 -6.28600100
2 3.20832100 6.24742800
Hg g
2 4.48529600 3.16920700
2 4.51320000 -3.23994500
END
dft
mult 2
xc pbe0
end
task sodft

之后稍作修改，得到Hg和I的PBE0-SODFT任务输入文件。计算后将能量求差，得到基于电子能量的BDE：
627.51*(-295.746562477964-153.684090186717+449.448365018831)=11.115 kcal/mol

如前面的图所示，HgI的解离能的三个不同来源的实验值为7.8、8.1、8.9 kcal/mol，当前算的和哪个都想差甚远，因此PBE0对此体系不够给力。对这种情况，我们可以在DFT级别计算出旋轨耦合对BDE的校正，然后加到CCSD(T)/def2-QZVP这样只考虑标量相对论的高计算级别得到的解离能上。为此，我们把上面用的HgI、Hg、I输入文件里的sodft改成dft（之后SO段落可以删掉，不删也无所谓），这样计算就只利用标量势部分了，旋轨耦合效应就不考虑了。结果为
627.51*(-295.697077663054-153.500765444841+449.222674994391)=15.582 kcal/mol
因此，旋轨耦合对BDE的校正量为11.115-15.582=-4.467 kcal/mol。

在CCSD(T)/def2QZVP级别算的HgI解离过程的电子能量变化：
627.51*(-153.2231386-297.2662532+450.5085777)=12.039 kcal/mol

用Gaussian在PBE0/def2-TZVP下做振动分析，得到常温下焓的热校正量对HgI键解离能的贡献：
627.51*(0.002360+0.002360-0.004277)=0.278 kcal/mol

put together，得到HgI的常温下的BDE：
12.039-4.467+0.278 = 7.85 kcal/mol
可见结果和实验符合得极好！

5 SODFT方式计算BDE总结

前面HgI的例子很有代表性，说明想准确计算重原子的键解离能，最简单省事的过程就是：
1 用较合适的泛函，在def2-TZVP或相似级别的结合相对论赝势的赝势基组（如cc-pVTZ-PP，但不划算）下进行优化和做振动分析，得到焓的热校正量对BDE的影响。注意应考虑ZPE校正因子
2 用较合适的泛函，在1的结构下用dhf-TZVP-2c赝势基组与配套的MDF标量势+旋轨势做SODFT计算，再去掉旋轨势做普通DFT计算，利用差值得到旋轨耦合对BDE的影响
3 基于1的结构，在尽可能高的级别下计算考虑了标量相对论效应的单点，由此得到基于电子能量算的BDE。体系很小时计算级别一般用CCSD(T)结合def2-QZVP或cc-pVQZ-PP赝势基组，赝势只考虑标量势部分。可以把结果再外推到CBS。
最后把1、2、3相加，就得到了特定温度下的键解离能。

上面说的是体系只含第五、六周期s,d,p族元素的情况。对于体系存在其它元素时，笔者认为应当这样考虑：
对前三周期的元素，就用全电子基组就行，不需要考虑相对论效应。
对第四周期元素，考虑相对论效应有益。分为两种情况：
(a)Cu之前的：Stuttgart赝势没有给出这些元素的旋轨势，cc-pVnZ-PP也没有给出这些元素的定义，def2对这些还是全电子基组。要考虑相对论效应就用Stuttgart赝势结合其标配赝势基组就完了。非要也考虑旋轨耦合那就用CRENB标量势+旋轨势结合CRENBL赝势基组吧。
(b)Cu~Kr：用cc-pVnZ-PP赝势基组，结合对应的MDF标量势和旋轨势。从EMSL上取cc-pVnZ-PP定义的时候赝势部分只有标量势部分，旋轨势得从Stuttgart赝势的官网 http://www.tc.uni-koeln.de/PP/clickpse.en.html上自行取，输出格式必须选molpro，要选小核的MDF版本（比如Br要选ECP10MDF）。输出的赝势里前几行是标量势（和EMSL上cc-pVnZ-PP直接带的一致），后几行是旋轨势。
对于镧系、锕系及一些第七周期的元素，就用Stuttgart赝势官网上小核标量势+旋轨势结合标配的赝势基组。情况较复杂。有的有MWB有的有MDF有的都有（优先用后者），有的有旋轨势有的没有旋轨势（没有的话就没辙了）。

另外，上面说的第1步的优化+振动分析，如果求准确，可直接用SODFT来做，但是由于SODFT只有半数值频率，体系稍大一点就会极为吃力。对于第3步高精度的考虑标量相对论的单点，不是必须用相对论赝势，用高质量全电子基组并使用较好的标量相对论哈密顿（LUT-IOTC、DKH3等）也可以，只不过耗时会高不少而且精度也未必更好。