Gaussian型Cube格点文件分析、运算程序GsGrid V1.6
注意:GsGrid的全部功能早已经融合到了Multiwfn (//www.umsyar.com/multiwfn)当中作为主功能13,故GsGrid不再更新。
GsGrid V1.6
Extract data from Gaussian grid file and grid file calculation
Programmed by Sobereva, 2009-Oct-7
Bug report or recommend: Sobereva@sina.com
1. 更新记录:
V1.0 最初版本,包含前四项功能。
V1.1 将输入输出单位由以前的波尔半径改为埃。加入了输出一定范围内平面的平均值的功能。
V1.3 修正了以前版本严重bug(即提取XZ平面数据得到的结果有时会偏差较大),新增功能8、功能9,用于得到自定义平面的格点数据。
V1.4 提高了output.txt中的数据输出精度(坐标精度不变),小数部分扩展为15位(整数部分最大5位),加入了格点文件计算功能。
V1.5 修正格点文件类型判断方式,使cube关键字生成的分子轨道格点文件可直接被gsgrid正确读取。新增支持多分子轨道格点文件。
V1.5.1 修正一个载入某些格点文件时出错的bug。
V1.5.2 修正读取多MO的格点文件失败的bug。
V1.6 加入了提取等值面上格点的功能,并可以将另外格点文件投影到某等值面上
2. GsGrid简介
Gaussian 提供了cubegen工具,以及cube、prop选项可以得到格点文件。缺点是数据点没有对应的坐标信息,而且也无法提取某个平面的数据作图。虽然支持 格点文件的可视化软件很多,GaussView较新版本及ChemCraft可以直接显示某个自定义平面上的等值线(前者支持)或填色图(后者支持),但 是程序自建绘图功能极为有限,较为粗糙,不适合作为文献插图,无法导出数据在专业作图软件中自定义绘制,另外这两个软件也是收费的。至于molden,没 有纯粹的windows版本,界面颇不友好。GsGrid主要为解决这些问题制作。
对于格点运算,虽然ChemCraft和cubman都能实现,但是所支持的运算操作各有不足,gsgrid从v1.4开始支持丰富的格点运算操作,范围超过ChemCraft和cubman支持操作的并集。
虽 然很多软件,如果gaussview、Moliso等都可以将某个属性投影到某个等值面上并以颜色表示数值大小,比如最常见的就是将分子静电势(MEP) 投影到电子密度为0.001的等值面,用以研究分子VDW表面的静电势。然而这些软件并不提供将等值面上的数值输出的功能,只能用颜色显示,GsGrid 弥补了这一不足。
2. GsGrid功能介绍
GsGrid目前支持6大类功能
第一类功能(程序中第1项):把格点文件的数据提取出来,附上每个数据点的坐标。见例1。
第二类功能(程序中第2-4项):选取指定的XY/YZ/XZ平面,得到这个平面上的数据点以便做图。见例2。
第三类功能(程序中第5-7项):将一定范围内平面的数据取平均输出,比如Z值在-3至3.5埃之间的平面的数据取平均输出。
第 四类功能(程序中第8-9项):通过指定三个原子,或者自行输入三个点的坐标,定义一个平面,得到此平面的上的格点数据。此平面上的数据点可以直接输出, 但是数据点并不在一个平面上,不方便做图。程序可以将此平面与XY平面的相交线做为轴,旋转此平面,使数据转移至XY平面,即此时数据点Z值皆为0,随后 可通过绘图软件做contour图。见例3。
第五类功能(程序中第10项):
格点文件中每个数据对某个常数进行加减乘除(子菜单1/3/5/7项)
格点文件中每个数据对另一个格点文件对应项进行加减乘除(子菜单2/4/6/8项)
格点文件中每个数据求幂(子菜单第9项);格点文件中每个数据对另一个格点文件对应项进行平方和、平方差、求平均操作(子菜单10/11/12项)
格点文件中每个数据求绝对值(子菜单第13项)
操作完毕后会输出新的格点文件,新的格点文件可继续使用gsgrid进行操作。见例4、例5。
第六类功能(程序中第11-12项):第11项功能为提取某个等值面上的格点。第12项功能能够将代表某个属性的格点文件A投影到格点文件B的数值所定义的等值面上,输出文件中包含这些等值面上的格点的坐标和A格点文件中坐标相对应的格点的数值。见例6、例7。
3. 例子
以下例子建议初学者从头看一遍。
例1:得到空间中每个坐标点的静电势
用高斯计算某个体系,写明%chk,然后用formchk将chk转换为fch,例如得到marioholic.fch。cubegen.exe在高斯目录下,将cubegen程序与marioholic.fch放到同一个文件夹,在dos中进入相应目录下运行:
cubegen 0 potential marioholic.fch aneta_langerova.cub 0 h
就得到了静电势格点文件aneta_langerova.cub。
(也可以在这个文件夹下用文本编辑器建立一个批处理文件,比如a.bat,内容就是上面这条命令,然后双击运行a.bat)
运行gsgrid,比如输入:(注:下文//后面皆代表注释,不要输入。换行处就是敲回车)
c:\aneta_langerova.cub //若.cub文件与gsgrid在同目录,只需输入文件名)
1 //功能1
即在相同目录下得到output.txt。里面包含aneta_langerova.cub里每个数据点的数值及其坐标。
------------------------------------
例2:画Z=0平面的电子密度图
先得到电子密度格点文件,运行:cubegen 0 density mizuki_nana.fch otoboku.cub -4 h
运行gsgrid,输入:
c:\otoboku.cub
2 //功能2,提取某XY平面的数据
0 //设定此XY平面的Z值为0
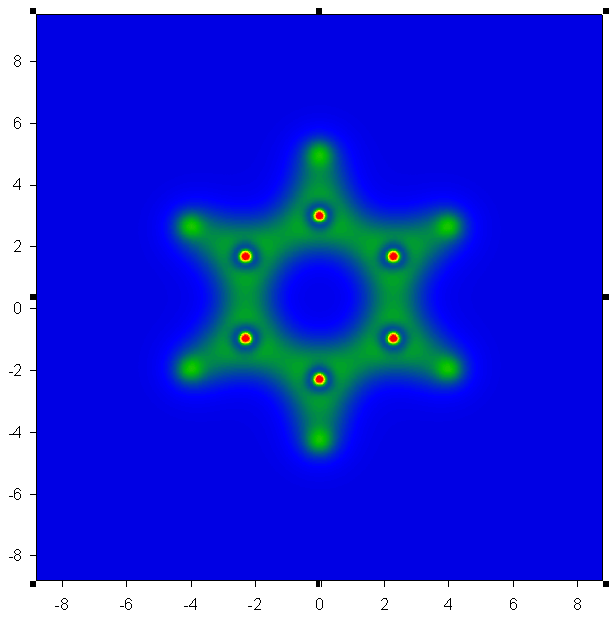
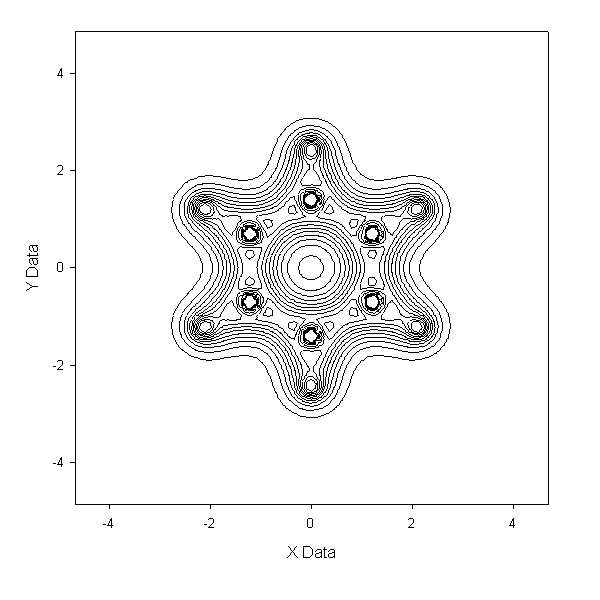
得 到output.txt,和例1一样。由于格点文件数据是离散的,故这里面的数据点只包含.cub中的Z值最接近于0的那个平面中的数据点。然后可以放到 sigmaplot等软件做图。以苯分子为例子(压缩包内c6h6.fch),以此法作图得到benzene-density.PNG及benzene- density-contour.GIF
再比如想得到X在-3.3至5.2范围内的YZ平面上的数据点的平均值,可使用程序第6个功能,运行gsgrid,输入
c:\otoboku.cub
6 //功能6
-3.3 5.2 //Z值范围
------------------------------------
例3:得到三个原子定义的平面的静电势图
设某个分子有三个原子编号为3、6、7,想得到这三个原子定义的平面上的静电势图,但是这三个原子并不平行于XY/YZ/XZ,故不能用程序的2、3、4项功能通过例2的方法做图。在V1.3版中添加了任意平面做图可以实现这个目的。
cubegen 0 potential ethane.fch 1.cub -4 h //ethane.fch在附件中,这里使用fine格点,否则图像会破碎,见后面说明。
运行gsgrid,输入:
c:\1.cub
8 //功能8
3,6,7 //输入三个原子序号
0.014 //以0.014埃为格点-平面临界距离
y //将平面数据通过旋转投影到XY平面上
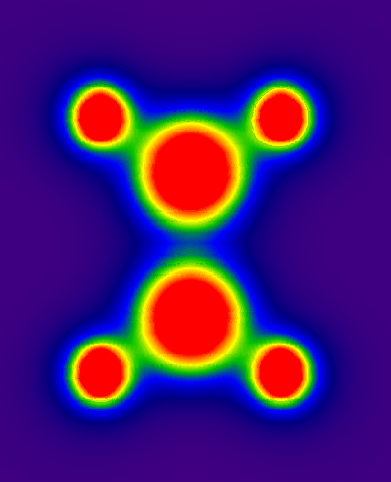
这样得到的结果就像例2,数据点z值皆为0,可以直接用绘图软件做图,使用sigmaplot得到的结果如附件中ethane-PES.PNG所示。
再比如想自定义三个点得到定义的平面的数据,运行gsgrid,输入:
c:\1.cub
9
2.3,1.1,2.55 //第1个点的XYZ
0.23,1.33,4.5 //第2个点的XYZ
0,-1.29,3.11 //第3个点的XYZ
0 //用默认的格点-平面临界距离
n //不投影至XY平面
------------------------------------
例4:得到某体系第4个分子轨道在某XY平面的密度分布
首先需要得到分子轨道波函数格点文件,运行cubegen 0 mo=4 divokej_bill.fch 1.cub 0 h。
求每个格点数据的2次方,因为波函数平方为概率密度。运行gsgrid,输入:
c:\1.cub
10 //第10项功能,即计算功能
9 //子菜单第8项功能,求幂
2 //设定指数,输入的数除了整数外,也可以是小数、负数。要注意底数是负数时指数须为整数,否则结果为NaN。
z.cub //输出的格点文件,不写路径则生成在当前路径下
假设这个分子轨道由两个电子占据,故每个格点数据应再乘以2,再次启动gsgrid,输入:
z.cub
10 //第10项功能,即计算功能
5 //子菜单第5项功能,乘以一个常数
2 //每个格点数据乘以2
lusaint.cub //输出的格点文件
最后再启动gsgrid,提取lusaint.cub的某XY平面数据即可,见例1。
再例如我们想得到mo=4和mo=5两个分子轨道上占据的电子密度和的格点文件。mo=4的格点文件仍是上面的1.cub,mo=5的格点文件是2.cub。运行gsgrid
1.cub //先输入第一个格点文件
10 //第10项功能,即计算功能
10 //子菜单第10项功能,求平方和,即A^2+B^2
2.cub //第二个格点文件
Bakuretsu_Tenishi.cub //输出的格点文件
若每个轨道是双占据的,再把Bakuretsu_Tenishi.cub用gsgrid乘以常数2即可。
实际上用gsgrid把1.cub和2.cub单独求平方,然后再相加得到的结果和上面一样,这里用子菜单第10项功能是因为比较方便,只需要一步而不必三步。
要注意,两个格点文件间运算,两个格点文件必须是相同体系,有相同的格点数目。
------------------------------------
例5:多分子轨道格点文件的读取
每 个高斯格点文件可以包含多个轨道,从gsgrid V1.5开始支持这样的格点文件。这里仍然使用例4中的第二个例子,需要获得MO=4和MO=5的总电子密度格点文件。为了方便,我们现在把mo=4和 mo=5的格点都写进一个文件里,例如cubegen 0 mo=4,5 bitboys.fch sob.cub 0 h。运行gsgrid,输入
sob.cub
1 //选取的格点文件若包含多个轨道信息,则会出现选择轨道的提示。这里输入1代表选择第一条轨道,即MO=4
10 //第10项功能,即计算功能
10 //平方和运算
sob.cub //第二个格点文件,因为MO=5的轨道就在sob.cub中,所以仍用sob.cub
2 //选格点文件中第二条轨道,即MO=5
z.cub //输出文件
闭壳层体系时再把z.cub的内容乘2即可。这样将多条轨道合并在一个格点文件中用起来比较方便,但是会造成格点文件成倍增大,gsgrid读取也会变慢。
第一个格点文件和第二个格点文件可以包含的轨道数目不同,也可以不是一类内容,如分子轨道与电子密度值,只要格点在数目、空间位置上是对应的即可。
使用gsgrid也可以提取多分子轨道格点文件中某一个轨道的格点文件,即选择那条轨道,使用比如加0或者乘以1的运算。
高 斯的分子轨道(包括多分子轨道)的格点文件与其它类型格点文件的主要区别在于前者的原子数为负,在原子坐标后面会加入分子轨道信息(见后面附带的格点文件 格式说明)。如果第一个格点文件是分子轨道格点文件,则运算后生成的新格点文件也将是分子轨道类型。若格点文件中原子数为正/负,则必须无/有分子轨道信 息,否则格点文件无法被gsgrid正确处理。
------------------------------------
例6:提取某个等值面的数据点
这个例子要用到1.6加入的功能11。下面我们要得到自带的test文件夹下c6h6.fch体系(苯,3-21G)的第19个分子轨道波函数的绝对值为0.02的等值面的格点。首先得到第19个分子轨道的格点文件:
cubegen 0 mo=19 c6h6.fch c6h6-mo-19.cub -3 h
使用功能11、12时最好使用中等及以上精细度的格点文件,所以这里使用-3参数即中等精细度。
运行gsgrid,依次输入:
c6h6-mo-19.cub
11 //第11项功能,提取某个等值面的格点
0.02,0.02 //这两个数分别定义下界和上届的数值,如果某格点的数值在这个范围内,则这个格点就会输出到output.txt。这里上界和下届输入的数值一样,则程 序会将这个数值的±3%作为上下界,即提取0.0194至0.0206范围内的格点(若不允许有±3%的偏差,得到的数据点太少)。
现在得到了output.txt,但这里只有分子轨道波函数为正值的部分,我们还想得到等值面为-0.02的格点,故把刚才得到的output.txt备份,再次在gsgrid中运行上述命令,0.02,0.02替换为-0.02,-0.02即可。
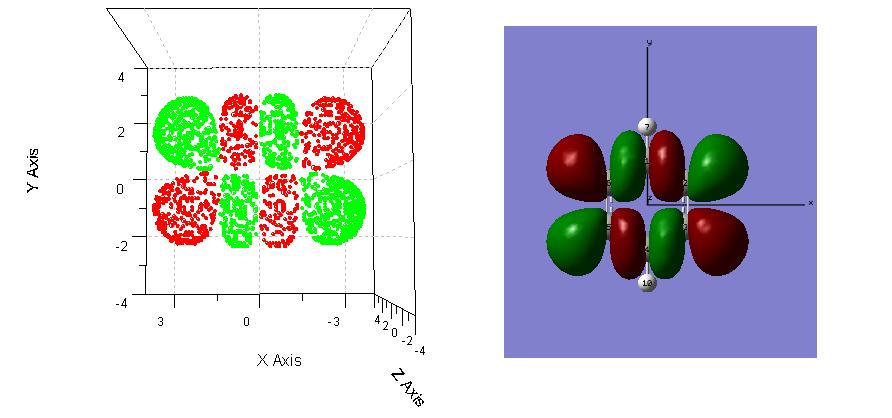
现在我们将这些格点放到origin里面做三维散点图,正值与负值部分分别用红色和绿色表示,得到了isosurface.PNG文件的左图。可以看到,我们提取的等值面上的格点是正确的,形状与gaussview中显示的此分子轨道波函数的0.02的等值面完全一致。
------------------------------------
例7:将静电势投影到电子密度为0.001的等值面
首先分别得到电子密度和静电势的格点文件,注意它们必须拥有相同格点数,每个格点坐标相等。
cubegen 0 density c6h6.fch c6h6-m-density.cub -3 h
cubegen 0 density c6h6.fch c6h6-m-eps.cub -3 h
运行gsgrid,依次输入:
c6h6-m-density.cub //通过这个格点文件确定等值面的格点
12 //选功能12
0.001 //等值面数值为0.001
4 //设定上下限偏差,用百分数表示。这里即设定数值在0.001±4%范围内的格点看做等值面格点
c6h6-m-eps.cub //将这个静电势格点文件投影到刚才设的等值面上并输出
这样我们得到的output.txt中的数据点的坐标就是c6h6-m-density.cub文件中数值为0.001±4%范围所定义的等值面上的格点的坐标,而这些点的数值就是c6h6-m-eps.cub文件中坐标相对应的点的数值。
------------------------------------
关于功能8和功能9的细节说明:
由 于格点文件的数据点在空间上是规律排布的,若自行定义一个平面,数据点显然不会恰好在平面上。所以想得到某个平面上的数据,就必须将平面附近的数据点投影 到平面上。在gsgrid中,只有数据点与平面垂直距离小于“格点-平面临界距离”的数据点才会被投影,符合要求的数据点投影的方法是沿着法线方向移动至 平面。格点-平面临界距离的设定会影响实际效果,一般用默认值即可(输入0使用建议值)。
有时通过这种投影方法获得的某平面的数据在做等值 线图时会发现图像虽然形状正常,但略有破碎,或者个别点数据怪异。此时可降低格点-平面临界距离来解决,例如改为默认值的1/2、1/4再重新做图,但是 格点-平面临界距离如果太近的话,投影到平面上的格点数太少,图像会变得粗糙。最好的解决方法是生成格点文件时使用fine格点,此时格点密度加大,投影 到平面上的数据准确度较好,可消除图像破碎问题,此时建议将格点-平面临界距离设为推荐值的1/2。
有时得到的等值线图有棱有角,是因为格点文件不够精细造成,亦可通过使用fine格点解决,也可以通过改变等值线或色彩范围、调节格点-平面临界距离来得到一定改善。
将平面的数据转移至XY平面的过程,是以自定义平面与XY平面的交线为轴,旋转自定义平面来实现的。不会使平面上数据得到的图像有任何变形,相当于眼睛垂直于自定义平面观看。
如果定义的平面与XY/YZ/XZ平面平行,程序会予以提示,此时请分别用2、3、4项功能代替,以得到更好结果。
关于8、9项功能使用若有问题或结果异常,请E-mail来信。
4. 使用注意
使用cubegen时,末尾一定要用h参数。
cubegen倒数第二个参数可以是-2,-3 和-4 分别对应于关键字Coarse,Medium和Fine。用了fine文件会很大,gsgrid读取也比较慢,但相应地数据点更精细,建议绘制文献图时使用fine。若设为0用默认值,大约与Medium相当。
gsgrid目前只支持X、Y、Z平移向量与坐标轴X、Y、Z平行的格点文件,即一般情况下的格点文件。
格点文件中所用单位为波尔半径,等于0.529177249埃,读入VMD、gaussview后会被转换为埃。为了与可视化程序保持一致,本程序在读入格点文件时已经将单位转换为埃,输入参数和输出结果都以埃为单位。
5. 使用技巧:
若想使程序以silent模式运行,也就是敲一个命令即完成指定任务,不必每一步都手动输入,可以编辑一个文件,比如batch.txt,内容如下:
1.cub
8
3,6,7
0.014
y
[空行]
[空行]
这样只要运行gsgrid < batch.txt,就可以完成例3中的任务,每一步都根据batch.txt的内容自动输入了。如果处理很多格点文件,这样会方便很多。
6. 附录
Gaussian格点文件格式简介:
例如水的静电势的格点文件
Title Card Required potenial //Title,不被gsgrid处理
Electrostatic potential from Total SCF Density //Title,不被gsgrid处理
3 -4.970736 -4.970736 -4.761332 //原子数(如果是分子轨道格点文件原子数为负值) 原点的X/Y/Z坐标
80 0.125841 0.000000 0.000000 //第一个“坐标轴”上有80个数据点,每个数据点间隔为0.12584波尔半径
80 0.000000 0.125841 0.000000 //第二个“坐标轴”
80 0.000000 0.000000 0.125841 //第三个“坐标轴”
8 8.000000 0.000000 0.000000 0.209404 //原子序号(氧),电子数,X/Y/Z坐标
1 1.000000 0.000000 1.481500 -0.837616
1 1.000000 0.000000 -1.481500 -0.837616
//若是分子轨道格点文件,这里有分子轨道信息。第一个数字为格点文件包含的分子轨道的数目,接下来是每个分子轨道的序号。例如3 1 5 7就是代表格点文件含3个分子轨道,分别是1、5、7号。分子轨道信息内容中每10个数字换一行。
7.33384E-03 7.33602E-03 7.33151E-03 7.31988E-03 7.30070E-03 7.27354E-03 //每个点的数据,每六个换一行,E13.5格式。如果数据点数不是6的倍数,最低维循环后不足6个数据位置的地方会留空。
7.23796E-03 7.19353E-03 7.13981E-03 7.07636E-03 7.00279E-03 6.91867E-03
6.82364E-03 6.71732E-03 6.59939E-03 6.46955E-03 6.32753E-03 6.17312E-03
......
这些数据点数据输出的循环次序是:最低维=第三个“坐标轴”(此例即是Z轴),中维=第二个“坐标轴”,最高维=第一个“坐标轴”。
数据点与其对应的坐标关系是:
a(i,j,k)%x=originx+trans1x*(i-1)+trans2x*(j-1)+trans3x*(k-1)
a(i,j,k)%y=originy+trans1y*(i-1)+trans2y*(j-1)+trans3y*(k-1)
a(i,j,k)%z=originz+trans1z*(i-1)+trans2z*(j-1)+trans3z*(k-1)
trans1/x/y/z代表第一个“坐标轴”三个分量,(或曰:格点的平移矢量)
trans2/x/y/z代表第二个“坐标轴”三个分量
trans3/x/y/z代表第三个“坐标轴”三个分量
originx/y/z代表原点位置
i、j、k代表某点在各个“坐标轴”上的数据点序号。
如果用cubegen默认设置,一、二、三号坐标轴实际上就相当于笛卡尔坐标轴X/Y/Z,彼此正交。
如果手动设置网格,可以自定义“坐标轴”的方向,不平行于笛卡尔坐标轴,但这种情况gsgrid只能提取全部数据点(第一个功能),不能提取指定平面的数据点。
也可以用cube、prop关键字生成格点文件,参见高斯手册,格式与cubegen生成的一样,但更建议使用cubegen来做。